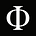Termodynamika a czasoprzestrzeń (3+1)
O zagadce czasoprzestrzeni (3 + 1)
Ostatnio rozmyślałem nad zagadką czasoprzestrzeni o wymiarach (3 + 1), którą obserwujemy w naszym Wszechświecie. Wcześniej doszedłem do wniosku, że znana nam matematyka jest stała, a nawet jeśli wszystkie możliwe kombinacje czasoprzestrzeni (X + Y) istnieją, tylko opcja (3 + 1) może prowadzić do powstania inteligentnych obserwatorów.
Jednak przyznaję, że istnieją inne możliwości. Jednym eleganckim rozwiązaniem jest powiązanie obserwacji, że czasoprzestrzeń (3 + 1) ma niemal minimalną liczbę wymiarów, z różnymi naturalnymi procesami minimalizującymi energię. Istnieje wiele przykładów takich procesów. Oto niektóre z nich:
Atomy tworzą cząsteczki, przyjmując konfiguracje minimalizujące energię potencjalną.
Bańka mydlana przybiera kształt minimalizujący napięcie powierzchniowe.
Ładunki elektryczne rozmieszczają się tak, aby zminimalizować całkowitą energię potencjalną układu elektrostatycznego.
Kryształy przyjmują strukturę sieciową, która reprezentuje stan minimalnej energii.
Zatem systemy fizyczne mają tendencję do minimalizowania energii. Ale jak połączyć to z liczbą wymiarów czasoprzestrzeni? Możliwy mechanizm zaproponowano w pracy zatytułowanej "Is the (3 + 1)-d nature of the universe a thermodynamic necessity?1". Autorzy wskazują, że czasoprzestrzeń jest powiązana z termodynamiką poprzez strzałkę czasu. Czas ma wyznaczony kierunek – od przeszłości do przyszłości – ponieważ prawa termodynamiki mówią, że entropia w układach zamkniętych (prawie) nigdy nie maleje.
Autorzy pracy proponują następujący scenariusz:
Na początku Wszechświat miał tylko jeden wymiar przestrzenny. Zgodnie z drugą zasadą termodynamiki, Wszechświat zmierza do wzrostu entropii.
Ta tendencja do wzrostu entropii powoduje optymalizację warunków termodynamicznych (gęstości potencjału Helmholtza), co prowadzi do zwiększania liczby wymiarów przestrzennych – najpierw do dwóch, a następnie do trzech.
Gdy Wszechświat osiąga trzy wymiary przestrzenne, gęstość potencjału Helmholtza osiąga optymalną wartość. Trójwymiarowa przestrzeń pozwala na stabilną, długoterminową dyspersję energii i rozwój złożonych struktur.
Druga zasada termodynamiki działa jako bariera przeciw dalszemu zwiększaniu liczby wymiarów przestrzennych, ponieważ byłoby to nieoptymalne z perspektywy wzrostu entropii – niestabilne struktury rozpraszają energię mniej efektywnie.
W tym przykładzie energia jest bardziej fundamentalna niż czasoprzestrzeń i zdolna do modelowania jej zgodnie ze swoimi „potrzebami,” które obejmują możliwie najefektywniejsze rozpraszanie energii. W takim przypadku minimalna czasoprzestrzeń byłaby naturalnym przejawem dążenia rzeczywistości fizycznej do optymalizacji warunków termodynamicznych w celu osiągnięcia stabilnego stanu.
Nawet jeśli zaakceptujemy to rozwiązanie zagadki czasoprzestrzeni (3 + 1), nie unieważnia ono moich wcześniejszych wniosków. Znana nam matematyka i prawa fizyki wciąż byłyby z jakiegoś powodu wyjątkowe. Gdyby było inaczej, można by wyobrazić sobie nieskończoną liczbę Wszechświatów, które przy różnych prawach fizyki optymalizowałyby czasoprzestrzeń do (4 + 1), (5 + 1), (6 + 1)... (N + 1) wymiarów przestrzennych, zamiast (3 + 1). W takim przypadku niemożliwe byłoby wyjaśnienie, dlaczego obserwujemy dokładnie (3 + 1), a nie jakąkolwiek inną dowolną liczbę wymiarów.
Tekst w języku angielskim: Thermodynamics and (3+1)-spacetime
[gr-qc/1502.01843v2] Is the (3 + 1) − d nature of the universe a thermodynamic necessity?